哈希表(Hash Table)
哈希表的一般原理
哈希表的参照物是数组或者链表,在后者中取值或者查找总是避免不了一个循环操作,造成O(n)的开销,通过构建哈希表可以将此类操作开销降低到O(1)。
典型哈希表的流程如下
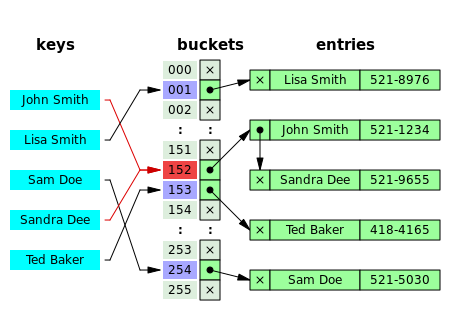
这是一个电话号码簿,以人名作为键值(key),将 key 值代入哈希函数得到 hash 值,通过 hash 值得到数组下标,通过下标可以在电话号码数组里直接得到号码。
为了这一高效过程付出的代价是
- 哈希函数的开销,该函数必须控制计算量
- 如果存储 hash 值,要付出额外的空间开销,例如 java 为每一个类提供 hash 属性
- hash 表构建开销为O(n),不过这一开销是一次性的,能够被此后表的操作所摊还;不过频繁的重建表还是要避免的
此外哈希表还有两个问题
1.哈希函数的构造,主要是使得输出结果区间分配均匀,避免带来过多的哈希冲突
2.哈希冲突。上图红色部分就显示了一个 hash 冲突,两个不同的人名通过 哈希函数得到相同的 hash 值,导致他们有得到同一个电话号码的风险。
哈希冲突的两种解决方法
不管选怎样的哈希函数,Hash 冲突都是不可避免的。为了解决这一问题,建立哈希表时可以采用两种方法
- 分离链接法

buckets 中存放的元素都是链表,计算得到下标后获得此位置上的链表,将数据写入链表即可。发生 hash 冲突的数据一并都写入链表,查找时先在 buckets 数组中找链表,这一步开销是O(1),而后在链表里找数据。
这种方法需要遍历链表,这一部分开销与链表平均长度有关,可以等价于装填因子有关。一般而言,装填因子可以达到 1.
- 开放定址法

这种方法不在使用链表,发生冲突后在冲突位置往后寻找一个空位安放数据。寻找安置空位的方法有
- 线性探测 逐个探测表,直到查找到一个空单元,把散列地址存放在该空单元。
- 平方探测 相对线性探测,相当于探测间隔 i*i 个单元的位置是否为空。
- 伪随机探测
考虑将 {89,18,49,58,69} 插入到一个散列表,散列函数是简单的除10求余数,冲突处理采用开放定址线性检测,其过程如下
| 散列地址 | 空表 | 插入89 | 插入18 | 插入49 | 插入58 | 插入69 |
|---|---|---|---|---|---|---|
| 0 | 49 | 49 | 49 | |||
| 1 | 58 | 58 | ||||
| 2 | 69 | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | 18 | 18 | 18 | 18 | ||
| 9 | 89 | 89 | 89 | 89 | 89 |
如果采用平方定址法
| 散列地址 | 空表 | 插入89 | 插入18 | 插入49 | 插入58 | 插入69 |
|---|---|---|---|---|---|---|
| 0 | 49 | 49 | 49 | |||
| 1 | ||||||
| 2 | 58 | 58 | ||||
| 3 | 69 | |||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 8 | 18 | 18 | 18 | 18 | ||
| 9 | 89 | 89 | 89 | 89 | 89 |
插入 58 发生冲突,第一次寻址是偏移 1 位,但此位被占据,第二次寻址是 4 位,即所处位置。
开放定址的问题是随着表中元素的增多,插入寻址会变得越来越困难。当装填因子超过一定值后,插入新元素将变的不可能,这时就需要重新构造一个容积更大的哈希表,这个操作叫做再散列。使用分离链接法解决哈希冲突是没有这个问题的。
再散列后新表的大小一般是旧表的两倍。
对于开放定址法,荷载因子是特别重要因素。超过0.8,查表时的缓存不命中(cache missing)按照指数曲线上升。例如 Java 系统库限制荷载因子为0.75,超过此值将发生再散列。
哈希表的实现
Python 中的字典 dict ,Java 中的 HashMap 都采用哈希表实现,以提高效率。不同的是前者采用开放定址法,后者采用分离链接法。
Python 的字典
字典的使用
1 | teams = {"seriaA":"inter", "Liga":"Barça", "Premier":"Liverpool"} |
python的函数函数为 hash()
1 | hash("seriaA") // -6110547274228262006 |
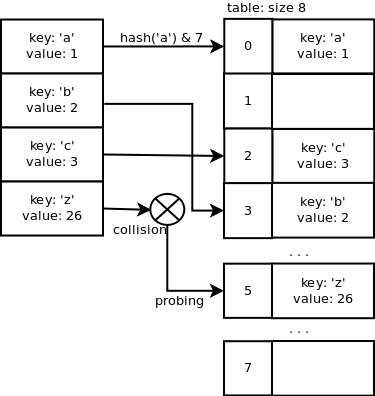
python 用一个数组来存储键/值对,其中键为索引值。索引的计算如下
1 | hash("seriaA") & (len-1) // len 是数组长度, & 运算等价于求余 |
Java 中的 HashMap
HashMap 的使用
1 | Map<String, String> map = new HashMap<>(); |
键值对存放的数组是
1 | HashMap.Node<K, V>[] table; |
其中 Node 定义如下,是典型的链表,说明 HashMap 采用的是分离链接法
1 | static class Node<K, V> implements Entry<K, V> { |
执行 put 操作的流程
1.首先利用下式计算出 key 对应的下标 i ,如果table中此位置无元素存在,那么创建 Node 节点并写入键值对即可
1 | hash(key) & (table.length-1) |
2.如果 table[i] 上已经有元素存在,遍历链表比对 hash值和key值,如果发现均相同的元素,则认为找到了元素,此时 put 的操作实际是 “修改已存在的元素“;如果没有找到,则此时 put 的操作实际是 “添加新元素。”
1 | Node.hash == hash && (Node.key == key || Node.key.equals(key)) |
上述条件说的是只要两个元素的 hash值相同且 至少满足equal 条件,即在 HashMap 中视为同一个元素。
ArrayMap
ArrayMap 与 HashMap 相比,是实现字典的另一种思路,它已经不采用哈希表来实现。它主要有两个数组
1 | int[] mHashes; //存放 hash 值的数组 |
它的 put 操作流程是
1.先计算hash值和下标
1 | hash = key.hashCode(); |
2.写入数据
1 | mHashes[index] = hash; // 下标是hash数组中的下标 |
可见键值对在数组中完全是并排存放的,而由hash值到下标的计算也不再使用哈希函数,而是将其按序排列使用二分查找,这步的开销是O(log(n)),比 HashMap 要大,但比数组要小。可以想见,在处理海量数据,例如城市居民通讯录时是不能采用这种结构的。
SparseArray
SparseArray 的使用如下
1 | SparseArray<String> array = new SparseArray<>(); |
主要存储结构如下,它的 key 和 value 是分开存放的,只不过 key 是特殊的 int 类型,设计这种结构是为了避免 Integer 类型的装箱和解装箱开销。
1 | private int[] mKeys; |
它的实现与 ArrayMap 类似,因为它的 key 直接是 int 类型,省去了计算 hash 值的过程。可以直接将 key 值在 mKeys 数组中进行二分查找,以获得下标。再用这个下标到 mValues 数组中获得对象。
哈希表的应用
哈希表最关键的特征是,将数组的查值变成O(1)开销,因此遇到类似问题,我们应该有意识的构建哈希表。但要注意,在具体实现过程中,可能碰到 key 键重复问题。
算法题:Two Sum
1 | """ |
常规解法是双循环,时间开销是O(n)。通过构建哈希表可以将其降低到O(1)。
1 | public int[] twoSum(int[] nums, int target) { |
这个解法利用了哈希表的高效查找。值得注意的是这里所构建哈希表的元素是(值,索引),因为索引不可能相同,而值可能相同,所以数组中的相同元素在插入时,会被覆盖。
例如
1 | int[] nums = {3, 3}; |
获得的 map 将是 { 3:1 }, 而不是{ 3:1, 3:0 } 。这样就存在一个隐患,所幸的是我们构建哈希表时被覆盖的是索引小的那个,查找时是根据索引小的那个查找索引大的那个,而且这个题目只要求查找出一对数就够了。
我们可以进一步思考下这个算法的关键步骤在哪里?
是利用哈希表判断差值是否在表中存在的那一步,这一步本来都要起一个循环来判断的,因为我们构建并利用了哈希表,所以开销从O(n)降低到了O(1),但是正因为如此,哈希表的 key 值必须用数字值而不是索引值,随之而来的就是重复数字值在哈希表中被覆盖问题,这导致了我们无法用这种方法求出所有满足条件的结果。

![[千与千寻的神隐]](/2019/09/14/工具/Hexo/timg.jpg)
